Personal Finance 101 — Achieving Financial Freedom
The Power of Compound Interest in Building Wealth

This article is adapted from a lesson I gave to 12th grade high school students at a non-profit I volunteer at called Minds Matter Seattle.
Time Value of Money
- Is it better to have $100 now or $100 one year from now?
Always better to have $100 now. Even putting your money in some boring, safe savings account with a ~3% yearly return rate will leave you with $103 after one year.
- Is it better to have $100 now or $110 one year from now?
If you can find an investment vehicle that yields more than a 10% yearly return rate, then take the $100 now. Otherwise, the guaranteed $110 one year from now is better.
The key takeaway is that there is value in having money now so that you can invest it and make it make money for you.
Here is a list of savings accounts that serve as examples of safe financial vehicles that can make your money make money for you.
Compound Interest
“Compound interest is the eighth wonder of the world.” ― Albert Einstein
Dictionary Definition: “Compound interest is defined as the interest calculated on the initial principal and also on the accumulated interest from previous periods.”
That last part is what makes compound interest the “eighth wonder of the world.” Let’s look at an example:
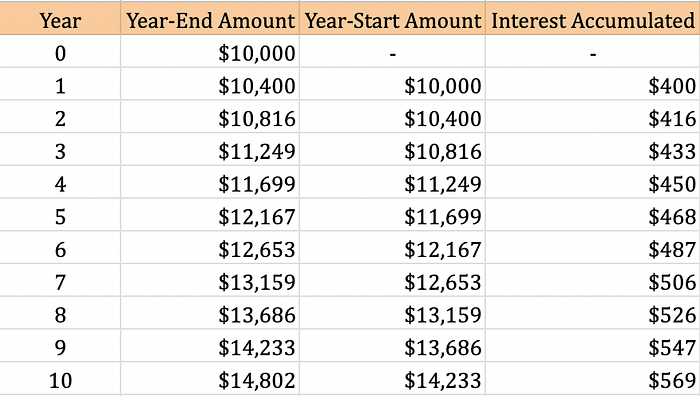
You have $10k and earn interest on it at an annual 4% rate.
After 1 year, this becomes $10,400 ($10k + $400 from interest). The magic happens when you don’t touch this money and allow interest to accumulate for 1 more year…
After 2 years, this becomes $10,816 ($10.4k from Year 1 + $416 in interest). That extra $16 is the magic. It is the extra interest earned by starting with $10.4k in Year 1 instead of the $10k starting amount.
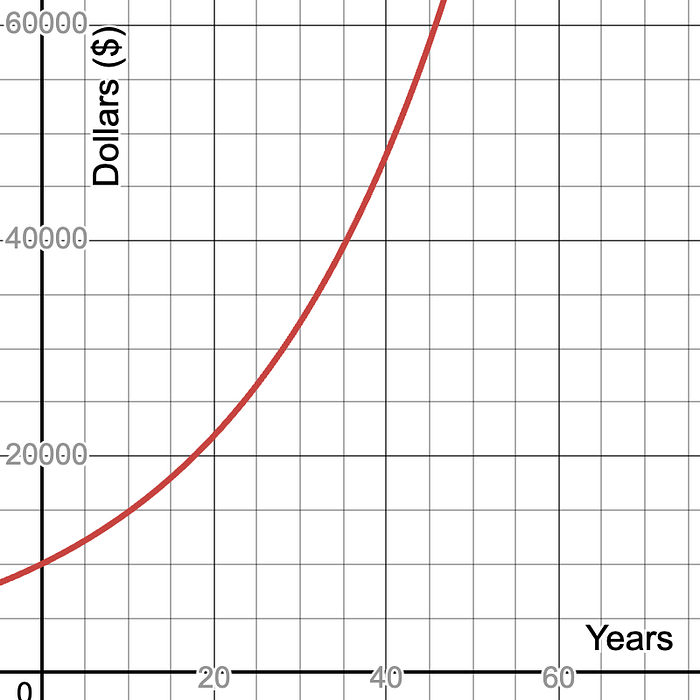
If the money is left untouched, the interest accumulated each year will grow at an exponential rate. The exponential nature of this pattern is what makes compound interest “magical”. Here is a table and chart that show the exponential nature of compound interest:
The Rule of 72
I’m intentionally avoiding mention of the Annual Compound Interest Formula to make this article feel less like a college lecture.
Instead, I will equip you with some simple heuristics to make sense of compound interest scenarios.
The Rule of 72 states that you simply have to divide 72 by the annual interest rate to approximate how many years it takes to double your money.
In the example from the previous section where you had $10,000 at a 4% annual interest rate, the Rule of 72 shows that it would take 18 years to double your money to $20,000.
Below, I’ve applied the Rule of 72 to various interest rates to give you an appreciation of the power of compound interest paired with a high interest rate:
- 2% interest rate → 36 years to double your money
- 4% interest rate → 18 years to double your money
- 6% interest rate → 12 years to double your money
- 8% interest rate → 9 years to double your money
How Much Money Do You Need To Retire?
For this section, let’s pretend you have $1M sitting in your bank account. How can you know if that is enough to retire?
The high-level strategy is putting your $1M in some financial vehicle that yields an annual interest rate high enough to cover your yearly living expenses while still maintaining enough money to get enough interest for your living expenses the following year.
Simplified Scenario
Let’s keep it simple and ignore inflation. For now, we will assume the price of all goods stays the same forever.
Let’s say you get a 3% annual interest rate on your $1M. In Year 0, let’s assume you have another way to cover your expenses for that year while you wait for interest to accumulate on the $1M. After 1 year, you will have your $1M starting amount plus $30k in interest. If your living expenses are $30k or below, you can retire. Even if you spend the full $30k, you will still have $1M leftover, which will earn 3% interest and give you $30k again the next year. Financial freedom has been achieved.
However, you can never dip into your $1M if you want this to work. The more you dip into your $1M, the less money you will get from your 3% interest to cover your yearly expenses.
Realistic Scenario
In the real world, inflation exists. In simple terms, inflation is the rate at which the price of the same goods increases year-over-year. By “goods” I’m referring to everything you need to live: food, housing, gas, electricity, smartphone, entertainment, travel, etc.
Inflation has a corrosive effect on your money. $1 today can buy more things today than $1 next year.
Inflation has historically been 2% in the United States, and we will use that value for this scenario. This means that you need $1.02 next year to buy the same things that $1 can buy today.
Let’s see how inflation impacts your retirement scenario:
- You get 3% annual interest rate on your savings of $1M, with an inflation rate of 2%.
- After 1 year, you have $1.03M.
- Just to keep up with inflation, you need to keep $1.02M.
- This leaves you with just $10k for your yearly living expenses.
Because of a 2% inflation, your 3% interest rate effectively becomes just a 1% interest rate. What is the impact of this? To maintain your same lifestyle of $30k in yearly expenses like in the Simple Scenario from before, you now need to have $3M to get the same $30k from a 1% interest rate. In this scenario, inflation effectively tripled how much you need to save!
The 4% Rule
To get even more realistic, we need to explicitly define which financial vehicles you are getting your annual interest rate from.
For any financial vehicle you consider, you need to subtract 2% from the listed annual interest rate to account for inflation. Also, you need financial vehicles that allow you to easily take out money every year for your living expenses (vehicles like CDs and bonds lock up your money until they mature).
To save you an exhaustive rundown of the pros/cons of various financial vehicles, I will continue with the most popular setup for personal finance scenarios — a mix of riskier US total stock market ETFs (like VTI) and safer fixed income vehicles like Bond ETFs (like BND). This mix has historically yielded 6–8% per year. After applying 2% inflation, this will yield 4–6% per year.
Assuming you use the mix of financial vehicles described above, the 4% Rule estimates that you can withdraw 4% of your savings every year for your living expenses, while still outpacing inflation and being able to withdraw 4% in following years forever.
If you have $1M to invest, you can assume that it will earn at least 6% in interest, and you can safely withdraw 4%, which is $40,000.
You can retire after saving $1M if your living expenses do not exceed $40,000 (due to the 4% Rule).
It’s also helpful to apply the 4% Rule in the opposite direction. To do this, estimate your yearly living expenses, and then multiply that amount by 25 to estimate how much you need to retire. For example, if my yearly living expenses are only $25k, I would need $625,000 to retire.
Let’s put all the teachings of this article together.
Compound interest is a magical vehicle for growing your savings at an exponential rate. Create wealth by making enough money to have enough left over each month to contribute to a financial vehicle that yields annual interest.
The “How Much Money Do You Need To Retire?” example showed a natural stopping point at which you achieve financial freedom and can safely keep and enjoy your wealth.
Generational wealth can be created by transferring your savings to your children when you pass away. Then, they can restart this process with a large starting amount so that they can build their wealth much faster via compound interest.
Of course, there are many roadblocks to having enough money to contribute to interest-yielding financial vehicles: having a high-paying job, minimizing expenses, etc. In the next article, we will cover the most crippling of these roadblocks: debt.
Disclaimer: The information provided in this article is for educational and informational purposes only. It should not be considered as financial or investment advice. Readers are encouraged to conduct their own research and consult with a qualified financial advisor before making any investment decisions. The author and publisher of this article shall not be held responsible for any actions taken as a result of the information presented herein.
